arctan1/x的导数

    arctan1/x的导数是-1/(1+x^2)。推导过程：[arctan(1/x)]'=1/[1+(1/x)^2]*(1/x)'=[x^2/(1+x^2)]*(-1/x^2)=-1/(1+x^2)

    

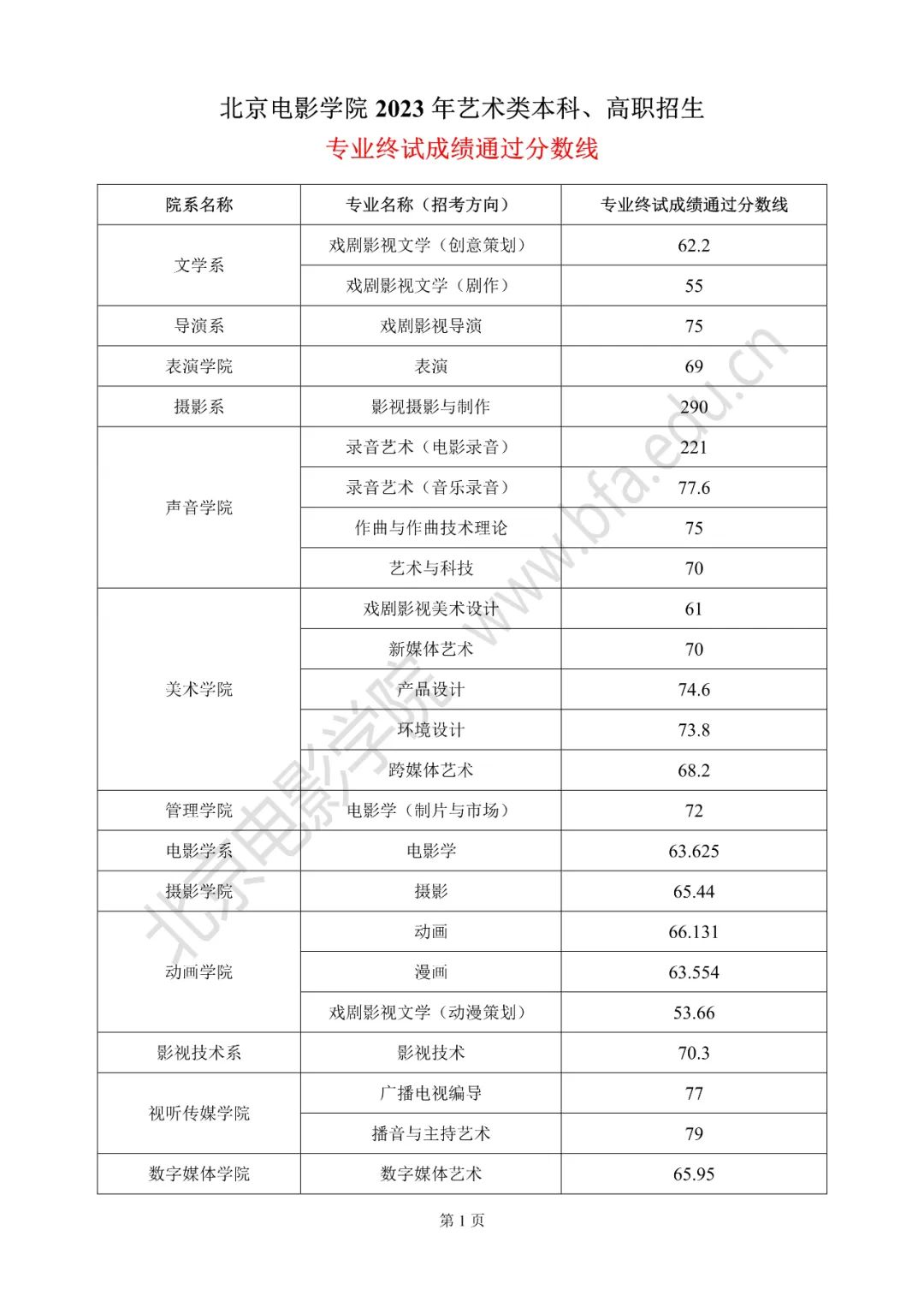
arctanx等于什么

    arctanx=1/(1+x2)。anx是正切函数，其定义域是{x|x≠(π/2)+kπ,k∈Z}，值域是R。arctanx是反正切函数，其定义域是R,反正切函数的值域为（-π/2,π/2）。

    推导过程：

    设x=tant，则t=arctanx，两边求微分

    dx=[(cos2t+sin2t)/(cos2x)]dt

    dx=(1/cos2t)dt

    dt/dx=cos2t

    dt/dx=1/(1+tan2t)

    因为x=tant

    所以上式t'=1/(1+x2)

    

反函数求导法则

    设原函数为y=f(x)，则其反函数在y点的导数与f'(x)互为倒数（即原函数，前提要f'(x)存在且不为0）。

    推导过程：

    设y=f(x),其反函数为x=g(y)

    可以得到微分关系式：dy=(df/dx)dx,dx=(dg/dy)dy

    那么,由导数和微分的关系我们得到

    原函数的导数是df/dx=dy/dx

    反函数的导数是dg/dy=dx/dy

    所以,可以得到df/dx=1/(dg/dx)